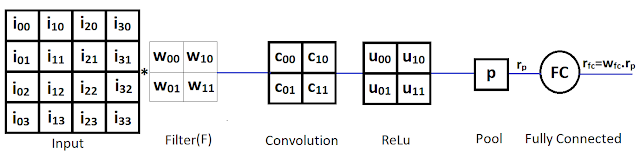
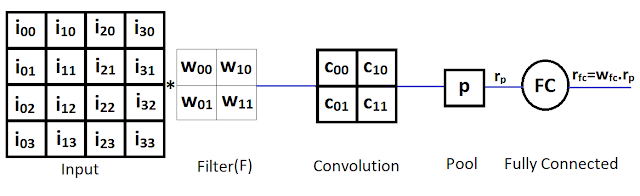
Part-III: A gentle introduction to Neural Network Backpropagation

In part-II , we derived the back-propagation formula using a simple neural net architecture using the Sigmoid activation function. In this article, which is a follow on to part-II we expand upon the NN architecture, to add one more hidden layer and derive a generic backpropagation equation that can be applied to deep (multi-layered) neural networks. This article attempts to explain back-propagation in an easier fashion with a simple NN, where each steps has been expanded in great detail and has explanations. After reading this text readers are encouraged to understand the more complex derivations given in Mitchell's book and elsewhere, to fully grasp the concept of back-propagation. You do need a basic understanding of partial derivatives and one of the best explanations are available in videos by Sal Khan at Khan academy . The neural network which has 1 input, 2 hidden and 1 output units(neuron) along with the sigmoid activation function at each hidden and output layer, is gi...