Part I: Backpropagation mechanics for a Convolutional Neural Network

In another article, we explained the basic mechanism of how a Convolutional Neural Network (CNN) works. In this article we explain the mechanics backpropagation w.r.t to a CNN and derive it value. We use the same simple CNN as used int he previous article, except to make it more simple we remove the ReLu layer. In part-II of this article we derive the backpropagation in the same CNN with the addition of a ReLu layer.

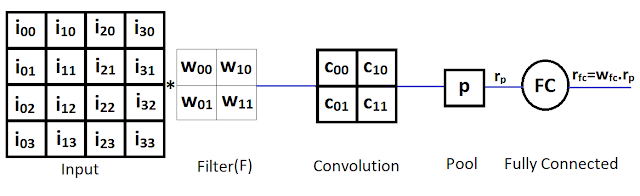
The CNN we use is given below:

In this simple CNN, there is one 4x4 input matrix, one 2x2 filter matrix (also known as kernel), a single convolution layer with 1 unit, a single pooling layer (which applied the MaxPool function) and a single fully connected (FC) layer. The elements of the filter matrix are equivalent to the unit weights in a standard NN and will be updated during the backpropagation phase.

Assuming a stride of 2 with no padding, the size of the convolution layer is determined by the following equation:

$$N={(W - F + 2.P)\over S} + 1$$
Here,
N: is the dimension (rows and columns) of the new(convolution) square matrix
W: is the dimension (rows and columns) of the input square matrix
F: is the dimension (rows and columns) of the filter square matrix
P: is the number of pixels(cells) of padding added
S: is the stride, or the number of cells skipped each time the kernel is slided

Putting these values in the equation,
$$\begin{align} N&={(4 - 2 + 2.0)\over 2} + 1\\ &=2 \end{align}$$
Hence the convolution layer will have a matrix of size 2x2.

The Error $E$ is defined as $E = {(t - r_{fc})^2\over 2}$, where t is given(expected) output in the training data.

We need find out change in $E$ in relation to the changes in values of weights $w_{fc}$ and $w_{00}$ through $w_{11}$ given in the filter.

Let us first find out how $E$ changes in relation to $w_{fc}$ or the rate of change of $E$ w.r.t. $w_{fc}$. This is also called the derivative of $E$ w.r.t $w_{fc}$ or $\partial E\over \partial w_{fc}$

$$\begin{align} E &= {(t - r_{fc})^2\over 2}\\ {\partial E\over \partial w_{fc}}&={\partial {(t - r_{fc})^2\over 2}\over \partial w_{fc}}\\ &={1 \over 2}.{\partial {(t - r_{fc})^2}\over \partial w_{fc}} \text{ ... eq.(1.1)}\\ \end{align}$$

---

As per the chain rule,:
$${dx \over dy}= {dx \over dz}.{dz \over dy}$$
For a partial derivative:
$${\partial x \over \partial y}={\partial x\over \partial z}.{\partial z\over \partial y}$$
Applying the chain rule to right term of eq.(1.1):
$$\text{Here, } z = {t - r_{fc}},x=z^2, \text{ and } y=w_{fc} \text{ ,therefore, }\\ \begin{align} {1 \over 2}.{\partial {(t - r_{fc})^2}\over \partial w_{fc}}&={1 \over 2}.{\partial x\over \partial y}\\ &={1 \over 2}.{\partial x\over \partial z}.{\partial z\over \partial y}\\ &={1 \over 2}.{\partial z^2\over \partial z}.{\partial z\over \partial y}\\ &={1 \over 2}.{\partial (t - r_{fc})^2\over \partial (t - r_{fc})}.{\partial (t - r_{fc})\over \partial w_{fc}}\\ &={1 \over 2}.{2(t - r_{fc})}.{\partial (t - r_{fc})\over \partial w_{fc}} \text{ ... eq.(1.2)}\\ \end{align}$$
Further,
$$\begin{align} {\partial (t - r_{fc})\over \partial w_{fc}}&={\partial (t - w_{fc}.r_p)\over \partial w_{fc}}\\ &={\partial t\over \partial w_{fc}} - {\partial w_{fc}.r_p\over \partial w_{fc}}\\ &={\partial t\over \partial w_{fc}} - r_p.{\partial w_{fc}\over \partial w_{fc}}\\ &=0 - r_p \text{ (as,} {\partial C \over \partial x}=0 \text { and } {\partial x \over \partial x}=1, \text {where C is a constant)},\\ \end{align}$$
Based on the above, in eq.(1.2),
$$\begin{align} {1 \over 2}.{\partial {(t - r_{fc})^2}\over \partial w_{fc}}&={1 \over 2}.{2(t - r_{fc})}.{\partial (t - r_{fc})\over \partial w_{fc}}\\ &={1 \over 2}.{2(t - r_{fc})}.{(0 - r_p)}\\ &=(t - r_{fc}).(-r_p) \end{align}$$

---

Therefore,
$$\begin{align} \partial E\over \partial w_{fc}&={\partial {(t - r_{fc})^2\over 2}\over \partial w_{fc}}\\ &={1 \over 2}.{\partial {(t - r_{fc})^2}\over \partial w_{fc}} \\ &=(t - r_{fc}).(-r_p)\\ \end{align}$$

Further upstream the only variables that control the value of $r_{fc}$ are in the filter F. Hence, we need to find out how E changes in relation to F or ${\partial E \over \partial F}$.

Since the pooling layer applies the MaxPool function, output $r_p$ of pooling layer is given as:
$r_p=max\{c_{00},c_{10},c_{10},c_{11}\}$The values of $c_{00},c_{10},c_{10},c_{11}$ are given as (see CNN article for more details):
$$\begin{align} c_{00}&={i_{00}.w_{11} + i_{10}.w_{01}+i_{01}.w_{10} + i_{11}.w_{00}}\\ c_{10}&={i_{20}.w_{11} + i_{30}.w_{01}+i_{21}.w_{10} + i_{31}.w_{00}}\\ c_{01}&={i_{02}.w_{11} + i_{12}.w_{01}+i_{03}.w_{10} + i_{12}.w_{00}}\\ c_{11}&={i_{22}.w_{11} + i_{32}.w_{01}+i_{23}.w_{10} + i_{33}.w_{00}}\\ \end{align}$$
Note that for the sake of simplicity, we do not normalize values of $c_{00},c_{10},c_{10},c_{11}$.

When you implement a CNN, the pooling layer has to remember the indices of the convolution layer filter maps that were used as output of the pooling. This is the approach that has been used in the Dasmic machine learning library. In this case, let us just assume that $c_{10}$ was the output of the pooling layer, or:
$$c_{10}=max\{c_{00},c_{10},c_{10},c_{11}\}\\ \Rightarrow r_p = c_{10} \text{ ... eq.(1.3)}$$
To compute ${\partial E \over \partial F}$, we will need to find out how E changes in relation to each element of matrix F, or we need to find,${\partial E \over w_{00}},{\partial E \over w_{10}},{\partial E \over w_{01}},{\partial E \over w_{11}}$.

Let us now compute, ${\partial E \over \partial w_{00}}$,

Applying the chain rule,
$$\begin{align} {\partial x \over \partial y}&={\partial x\over \partial z}.{\partial z\over \partial y}\\ \text{Here, } z = c_{10}, x&=E, \text{ and } y=w_{00} \text{ ,therefore, }\\ {\partial E \over \partial w_{00}}&={\partial E \over \partial c_{10}}.{\partial c_{10} \over \partial w_{00}} \text{ ... eq.(2.1)}\\ \end{align}$$
Solve for the right term ${\partial c_{10} \over \partial w_{00}}$ in eq.(2.1):
$$\begin{align} {\partial c_{10} \over \partial w_{00}}&={\partial ({i_{20}.w_{11} + i_{30}.w_{01}+i_{21}.w_{10} + i_{31}.w_{00})}\over \partial w_{00}} \text { (substituting value of c_{10})}\\ &={\partial {(i_{20}.w_{11})} \over \partial w_{00}}+ {\partial {(i_{30}.w_{01})} \over \partial w_{00}} + {\partial {(i_{21}.w_{10})} \over \partial w_{00}} + {\partial {(i_{31}.w_{00})} \over \partial w_{00}} \\ &={\partial {(i_{20}.w_{11})} \over \partial w_{00}}+ {\partial {(i_{30}.w_{01})} \over \partial w_{00}} + {\partial {(i_{21}.w_{10})} \over \partial w_{00}} + i_{31}.{\partial {w_{00}} \over \partial w_{00}}\\ \end{align}$$
Note that the terms $({i_{20}.w_{11}}), ({i_{30}.w_{01}})$ and $({i_{21}.w_{10}})$ will not change w.r.t $w_{00}$ hence, can be treated as a constant C
As, ${\partial C \over \partial x} = 0$
$$\begin{align} \partial c_{10} \over \partial w_{00}&={\partial {(i_{20}.w_{11})} \over \partial w_{00}}+ {\partial {(i_{30}.w_{01})} \over \partial w_{00}} + {\partial {(i_{21}.w_{10})} \over \partial w_{00}} + i_{31}.{\partial {w_{00}} \over \partial w_{00}}\\ &= 0 + 0 + 0 + i_{31}.{\partial {w_{00}} \over \partial w_{00}}\\ &= 0 + 0 + 0 + i_{31} (\text {as, }{\partial x \over \partial x}=0 \text {)}\\ &= i_{31} \text{ ... eq.(2.2)} \end{align}$$
Let us now find the left term of eq. (2.1) ${\partial E \over \partial c_{10}}$. As,
$E = {(t - r_{fc})^2\over 2}$, where t is given(expected) output in the training data,
$$\begin{align} {\partial E \over \partial c_{10}}&={\partial {(t - r_{fc})^2\over 2}\over \partial c_{10}} &={1 \over 2}.{\partial {(t - r_{fc})^2}\over \partial c_{10}} \text{ ... eq.(2.3)}\\ \end{align}$$
For a partial derivative:
$${\partial x \over \partial y}={\partial x\over \partial z}.{\partial z\over \partial y}$$
Applying the chain rule to right term of eq.(2.3):
$$\text{Here, } z = {t - r_{fc}},x=z^2, \text{ and } y=c_{10} \text{ ,therefore, }\\ \begin{align} {1 \over 2}.{\partial {(t - r_{fc})^2}\over \partial c_{10}}&={1 \over 2}.{\partial x\over \partial y}\\ &={1 \over 2}.{\partial x\over \partial z}.{\partial z\over \partial y}\\ &={1 \over 2}.{\partial z^2\over \partial z}.{\partial z\over \partial y}\\ &={1 \over 2}.{\partial (t - r_{fc})^2\over \partial (t - r_{fc})}.{\partial (t - r_{fc})\over \partial c_{10}}\\ &={1 \over 2}.{2(t - r_{fc})}.{\partial (t - r_{fc})\over \partial c_{10}} \text{ ... eq.(2.4)}\\ \end{align}$$
Further,
$$\begin{align} {\partial (t - r_{fc})\over \partial c_{10}}&={\partial (t - w_{fc}.r_p)\over \partial c_{10}}\\ &={\partial t\over \partial c_{10}} - {\partial w_{fc}.r_p\over \partial c_{10}}\\ \text { from eq.(1.3) we know,} r_p = c_{10} \text{,}\\ {\partial (t - r_{fc})\over \partial c_{10}}&={\partial t\over \partial c_{10}} - w_{fc}.{\partial c{10}\over \partial c_{10}}\\ &=0 - w_{fc} \text{ (as,} {\partial C \over \partial x}=0 \text { and } {\partial x \over \partial x}=1, \text {where C is a constant)},\\ \end{align}$$
Applying value of ${\partial (t - r_{fc})\over \partial c_{10}}$ in eq(2.4),
$$\begin{align} {1 \over 2}.{\partial {(t - r_{fc})^2}\over \partial c_{10}}&={1 \over 2}.{2(t - r_{fc})}.{\partial (t - r_{fc})\over \partial c_{10}}\\ &={1 \over 2}.{2(t - r_{fc})}.(0 - w_{fc})\\ &=(t - r_{fc}).(0 - w_{fc})\\ \end{align}$$
Applying value of ${1 \over 2}.{\partial {(t - r_{fc})^2}\over \partial c_{10}}$ in eq.(2.3),
$$\begin{align} {\partial E \over \partial c_{10}}&={\partial {(t - r_{fc})^2\over 2}\over \partial c_{10}} &=(t - r_{fc}).(0 - w_{fc})\\ &=(t - r_{fc}).(-w_{fc}) \text{ ... eq.(2.5)}\\ \end{align}$$

Applying values from eq.(2.2) and eq.(2.5) in eq. (2.1),
$$\begin{align} {\partial E \over \partial w_{00}}&={\partial E \over \partial c_{10}}.{\partial c_{10} \over \partial w_{00}} \text{ ... eq.(2.1)}\\ &={\partial E \over \partial c_{10}}.(i_{31}) \text { from eq.(2.2)} \\ &={(t - r_{fc}).(-w_{fc})}.(i_{31}) \text { from eq.(2.5) ... eq. (2.6)} \\ \end{align}$$

Using similar steps as for ${\partial E \over \partial w_{00}}$ let us now compute ${\partial E \over \partial w_{10}}$,

Applying the chain rule as before,
$$\begin{align} {\partial x \over \partial y}&={\partial x\over \partial z}.{\partial z\over \partial y}\\ \text{Here, } z = c_{10}, x&=E, \text{ and } y=w_{10} \text{ ,therefore, }\\ {\partial E \over \partial w_{00}}&={\partial E \over \partial c_{10}}.{\partial c_{10} \over \partial w_{10}} \text{ ... eq.(3.1)}\\ \end{align}$$
Solve for the right term ${\partial c_{10} \over \partial w_{10}}$ in eq.(3.1):
$$\begin{align} {\partial c_{10} \over \partial w_{10}}&={\partial ({i_{20}.w_{11} + i_{30}.w_{01}+i_{21}.w_{10} + i_{31}.w_{00})}\over \partial w_{10}} \text { (substituting value of} c_{10} \text {)}\\ &={\partial {(i_{20}.w_{11})} \over \partial w_{10}}+ {\partial {(i_{30}.w_{01})} \over \partial w_{10}} + {\partial {(i_{21}.w_{10})} \over \partial w_{10}} + {\partial {(i_{31}.w_{00})} \over \partial w_{10}} \\ &={\partial {(i_{20}.w_{11})} \over \partial w_{10}}+ {\partial {(i_{30}.w_{01})} \over \partial w_{10}} + i_{21}.{\partial {w_{10}} \over \partial w_{10}} + {\partial ({i_{31}.w_{00}}) \over \partial w_{10}}\\ \end{align}$$
Note that $({i_{20}.w_{11}}), ({i_{30}.w_{01}})$ and $({i_{31}.w_{00}})$ will not change w.r.t $w_{00}$ hence, can be treated as a constant C
As, ${\partial C \over \partial x} = 0$
$$\begin{align} \partial c_{10} \over \partial w_{00}&={\partial {(i_{20}.w_{11})} \over \partial w_{10}}+ {\partial {(i_{30}.w_{01})} \over \partial w_{10}} + i_{21}.{\partial {w_{10}} \over \partial w_{10}} + {\partial {i_{31}.w_{00}} \over \partial w_{10}}\\ &= 0 + 0 + i_{21}.{\partial {w_{00}} \over \partial w_{00}} + 0 \\ &= 0 + 0 + i_{21} + 0 \text { (as, }{\partial x \over \partial x}=0 \text {)}\\ &= i_{21} \text{ ... eq.(3.2)} \end{align}$$
Let us now find the left term of eq. (3.1) ${\partial E \over \partial c_{10}}$. As,
$(E = {(t - r_{fc})^2\over 2}$, where t is given(expected) output in the training data,
$$\begin{align} {\partial E \over \partial c_{10}}&={\partial {(t - r_{fc})^2\over 2}\over \partial c_{10}} &={1 \over 2}.{\partial {(t - r_{fc})^2}\over \partial c_{10}} \text{ ... eq.(3.3)}\\ \end{align}$$
For a partial derivative:
$${\partial x \over \partial y}={\partial x\over \partial z}.{\partial z\over \partial y}$$
Applying the chain rule to right term of eq.(3.3):
$$\text{Here, } z = {t - r_{fc}},x=z^2, \text{ and } y=c_{10} \text{ ,therefore, }\\ \begin{align} {1 \over 2}.{\partial {(t - r_{fc})^2}\over \partial c_{10}}&={1 \over 2}.{\partial x\over \partial y}\\ &={1 \over 2}.{\partial x\over \partial z}.{\partial z\over \partial y}\\ &={1 \over 2}.{\partial z^2\over \partial z}.{\partial z\over \partial y}\\ &={1 \over 2}.{\partial (t - r_{fc})^2\over \partial (t - r_{fc})}.{\partial (t - r_{fc})\over \partial c_{10}}\\ &={1 \over 2}.{2(t - r_{fc})}.{\partial (t - r_{fc})\over \partial c_{10}} \text{ ... eq.(3.4)}\\ \end{align}$$
Further,
$$\begin{align} {\partial (t - r_{fc})\over \partial c_{10}}&={\partial (t - w_{fc}.r_p)\over \partial c_{10}}\\ &={\partial t\over \partial c_{10}} - {\partial w_{fc}.r_p\over \partial c_{10}}\\ \text { from eq.(1.3) we know,} r_p = c_{10} \text{,} &={\partial t\over \partial c_{10}} - w_{fc}.{\partial c{10}\over \partial c_{10}}\\ &=0 - w_{fc} \text{ (as,} {\partial C \over \partial x}=0 \text { and } {\partial x \over \partial x}=1, \text {where C is a constant)},\\ \end{align}$$
Applying value of ${\partial (t - r_{fc})\over \partial c_{10}}$ in eq(3.4),
$$\begin{align} {1 \over 2}.{\partial {(t - r_{fc})^2}\over \partial c_{10}}&={1 \over 2}.{2(t - r_{fc})}.{\partial (t - r_{fc})\over \partial c_{10}}\\ &={1 \over 2}.{2(t - r_{fc})}.(0 - w_{fc})\\ &=(t - r_{fc}).(0 - w_{fc})\\ \end{align}$$
Applying value of ${1 \over 2}.{\partial {(t - r_{fc})^2}\over \partial c_{10}}$ in eq.(2.3),
$$\begin{align} {\partial E \over \partial c_{10}}&={\partial {(t - r_{fc})^2\over 2}\over \partial c_{10}} &=(t - r_{fc}).(0 - w_{fc})\\ &=(t - r_{fc}).(-w_{fc}) \text{ ... eq.(3.5)}\\ \end{align}$$

Applying values from eq.(3.2) and eq.(3.5) in eq.(3.1),
$$\begin{align} {\partial E \over \partial w_{10}}&={\partial E \over \partial c_{10}}.{\partial c_{10} \over \partial w_{10}} \text{ ... eq.(3.1)}\\ &={\partial E \over \partial c_{10}}.(i_{21}) \text { from eq.(3.2)} \\ &={(t - r_{fc}).(-w_{fc})}.(i_{21}) \text { from eq.(3.5) ... eq.(3.6)} \\ \end{align}$$
It will be clear by now that any ${\partial E \over \partial w_{xx}}$ is the term ${(t - r_{fc}).(-w_{fc})}$ multiplied by the element in the input matrix $w_{xx}$.Therefore for the remaining weights $w_{01}$ and $w_{11}$:
$$\begin{align} {\partial E \over \partial w_{01}}&={(t - r_{fc}).(-w_{fc})}.(i_{30}) \text { ... eq.(4.1)}\\ {\partial E \over \partial w_{11}}&={(t - r_{fc}).(-w_{fc})}.(i_{20}) \text { ... eq.(5.1)}\\ \end{align}$$
In the article on introduction to backpropagation, we study backprogagation mechanics for this simple NN:

Here,
$$\begin{align} {\partial E\over \partial w_h}&={(t - r_o)}.{(-w_o.i)}\\ \end{align}$$

The derivatives of ${\partial E \over \partial w_{00}},{\partial E \over \partial w_{01}},{\partial E \over \partial w_{10}}, {\partial E \over \partial w_{11}}$ are in the same format, wherein we multiply the the error between training example and computed output, by the weight of the downstream layer and the input.

Weight update rule:

Once the direction of the weight update is determined using ${\partial E \over \partial w_{xy}}$ for a weight $w_{xy}$, we update the weights based on the same rule as for a standard NN. Therefore,

If $\eta$ is the learning rate and controls the numeric value by which weights are changed:

The weights for FC layer ($w_{fc}$) layer will be updated as:
$$\begin{align} \Delta w_{fc}&=-\eta.{\partial E\over \partial w_{fc}}\\ &=-\eta.{(t - r_{fc}).(-w_{fc})}.(i_{31}) \text { (from eq.(1.6))} \\ &=\eta.{(t - r_{fc}).(w_{fc})}.(i_{31})\\ \Rightarrow w_{fc} &= w_{fc} + \Delta w_{fc} \end{align}$$
The weights for filter ($w_{00},w_{10},w_{01},w_{11}$) will be updated as:
$$\begin{align} \Delta w_{00}&=-\eta.{\partial E\over \partial w_{00}}\\ &=-\eta.{(t - r_{fc}).(-w_{fc})}.(i_{31})\text { (from eq.(2.6))} \\ &=\eta.{(t - r_{fc}).(w_{fc})}.(i_{31})\\ \Rightarrow w_{00} &= w_{00} + \Delta w_{00} \end{align}$$
$$\begin{align} \Delta w_{10}&=-\eta.{\partial E\over \partial w_{10}}\\ &=-\eta.{(t - r_{fc}).(-w_{fc})}.(i_{21})\text { (from eq.(3.6))} \\ &=\eta.{(t - r_{fc}).(w_{fc})}.(i_{21})\\ \Rightarrow w_{10} &= w_{10} + \Delta w_{10} \end{align}$$
$$\begin{align} \Delta w_{01}&=-\eta.{\partial E\over \partial w_{01}}\\ &=-\eta.{(t - r_{fc}).(-w_{fc})}.(i_{30})\text { (from eq.(4.1))} \\ &=\eta.{(t - r_{fc}).(w_{fc})}.(i_{30})\\ \Rightarrow w_{01} &= w_{01} + \Delta w_{01} \end{align}$$
$$\begin{align} \Delta w_{11}&=-\eta.{\partial E\over \partial w_{11}}\\ &=-\eta.{(t - r_{fc}).(-w_{fc})}.(i_{20})\text { (from eq.(5.1))} \\ &=\eta.{(t - r_{fc}).(w_{fc})}.(i_{20})\\ \Rightarrow w_{11} &= w_{11} + \Delta w_{11} \end{align}$$

Note that if the output of the pooling layer is different than $c_{10}$ you have to change the input values ($i_{xy}$) used in the weight update rule.

This concludes the derivation of backpropagation for our simple CNN. In part-II, we take a look how backpropagation is impacted by adding a rectified linear unit (ReLu) activation layer.