Part IV: Backpropagation mechanics for a Convolutional Neural Network

In part-III of this series, we derived the weight update equation for the backpropagation operation of a simple Convolutional Neural Network (CNN) using 3 inputs matrices representing the red, blue and green spectrum of an image. In this article, we derive the backpropagation with 2 consecutive convolution and ReLu layers, and subsequently derive a general backpropagation equation for deep-learning (multi-layered) CNN. To keep our equations simple (and readable), we revert back to only 1 input matrix. This CNN is similar to one used in part-II, except there are 2 convolution and ReLu layers.

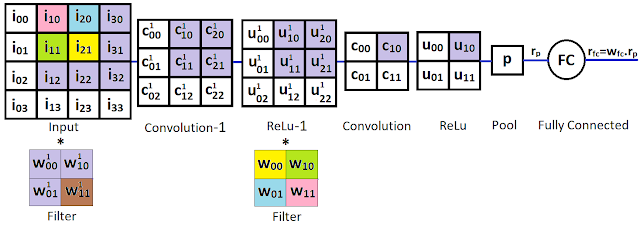
The CNN we use is represented by:

In this CNN, there are 1 4x4 input matrices, two 2x2 filter matrices (or kernels), two convolution layers , two ReLu layers, a single pooling layer (which applies the MaxPool function) and a single fully connected (FC) layer. The elements of the filter matrices are equivalent to the unit weights in a standard NN and will be updated during the backpropagation phase.

Assuming a stride of 1 with no padding, the size of the convolution layers is determined by the following equation:

$$
N={(W - F + 2.P)\over S} + 1
$$
Here,
N: is the dimension (rows and columns) of the new(convolution) square matrix
W: is the dimension (rows and columns) of the input square matrix
F: is the dimension (rows and columns) of the filter square matrix
P: is the number of pixels(cells) of padding added
S: is the stride, or the number of cells skipped each time the kernel is slided

Putting these values in the equation for the 1st convolution layer,
$$
\begin{align}
N&={(4 - 2 + 2.0)\over 1} + 1\\
&=3
\end{align}
$$
Hence the Convolution-1 convolution layer will have a matrix of size 3x3, which will serve as an input to the ReLu-1 layer with the same dimension. This 3x3 input layer will be the input matrix to the next downstream convolution, who's size is determined by the same equation. Hence for the 2nd convolution layer with a stride of 1,
$$
\begin{align}
N&={(3 - 2 + 2.0)\over 1} + 1\\
&=2
\end{align}
$$
Therefore, the second convolution layer will be of size 2x2, which is also the size of the downstream ReLu layer.

The Error \(E\) is defined as \(E = {(t - r_{fc})^2\over 2}\), where t is given(expected) output in the training data.

We need to find out the change in \(E\) in relation to the changes in values of weights of the FC layer, \(w_{fc}\), as well as weights of the filters, \(w_{00}^1\) through \(w_{11}^1\) and, \(w_{00}\) through \(w_{11}\).

In part-II, we used the following CNN:

Downstream of the ReLu-1 layer, the architecture of this CNN is same as the one we use in this article. Therefore the derivations of \({\partial E\over \partial w_{fc}},{\partial E \over \partial w_{00}},{\partial E \over \partial w_{10}},{\partial E \over \partial w_{01}}\) and \({\partial E \over \partial w_{11}}\) derived in part-II can be used here.

In part-II, we assumed that \(u_{10}\) is the result of the pooling layer (\(r_p = u_{10})\), based on which the following was derived:

$$
\begin{align}
{\partial E\over \partial w_{fc}}&=(t - r_{fc}).(-r_p) \text { ... eq.(1.1)}\\
{\partial E \over \partial w_{00}}&={(t - r_{fc}).(-w_{fc})}.{\partial u_{10} \over \partial w_{00}} \text { ... eq.(1.2)}\\
{\partial E \over \partial w_{10}}&={(t - r_{fc}).(-w_{fc})}.{\partial u_{10} \over \partial w_{10}} \text { ... eq.(1.3)}\\
{\partial E \over \partial w_{01}}&={(t - r_{fc}).(-w_{fc})}.{\partial u_{10} \over \partial w_{00}} \text { ... eq.(1.4)}\\
{\partial E \over \partial w_{11}}&={(t - r_{fc}).(-w_{fc})}.{\partial u_{10} \over \partial w_{11}} \text { ... eq.(1.5)}\\
\end{align}
$$
where,
$$
\begin{align}
u_{10}&=max(0,c_{10})\\
&\text{and,}\\
c_{10}&=u_{10}^1.w_{11} + u_{20}^1.w_{01}+u_{11}^1.w_{10}+u_{21}^1.w_{00}\\
&\text{hence,}\\
u_{10}&=max(0,{u_{10}^1.w_{11} + u_{20}^1.w_{01}+u_{11}^1.w_{10}+u_{21}^1.w_{00}})\\
\end{align}
$$
Notice that the values of \(c_{10}\) between part-II and here are different because the input matrix to the 2x2 convolution layer is not the same.

With values of \({\partial E\over \partial w_{fc}},{\partial E \over \partial w_{00}},{\partial E \over \partial w_{10}},{\partial E \over \partial w_{01}}\) and \({\partial E \over \partial w_{11}}\) known from previous work in part-II, we now have to find values of \({\partial E \over \partial w_{00}^1},{\partial E \over \partial w_{10}^1},{\partial E \over \partial w_{01}^1}\) and \({\partial E \over \partial w_{11}^1}\).

Since \(u_{10}\) is the result of the pooling layer, \(E\) will only be impacted by values that directly affect the values of \(u_{10}\). The following diagram highlights (in purple) all values in the CNN that affect the value of \(u_{10}\).

Note that in this CNN, \(c_{10}=u_{10}^1.w_{11} + u_{20}^1.w_{01}+u_{11}^1.w_{10}+u_{21}^1.w_{00}\)

Let us now compute \({\partial E \over \partial w_{00}^1}\),

Applying the chain rule,
$$
\begin{align}
{\partial x \over \partial y}&={\partial x\over \partial z}.{\partial z\over \partial y}\\
\text{Here, } z = u_{10}, x&=E, \text{ and } y=w_{00}^1 \text{ ,therefore, }\\
{\partial E \over \partial w_{00}^1}&={\partial E \over \partial u_{10}}.{\partial u_{10} \over \partial w_{00}^1} \text{ ... eq.(2.1)}\\
\end{align}
$$
Solving for the right term \({\partial u_{10} \over \partial w_{00}^1}\) in eq.(2.1):
$$
\begin{align}
{\partial u_{10} \over \partial w_{00}^1}&={\partial (max(0,c_{10})) \over \partial w_{00}^1} \text{ ... eq.(2.2)}
\end{align}
$$
Now,
$$
{d {{max(0,x)} \over {dx}}}=
\begin{cases}
x, & \text {if x > 0}\\
0, & \text {if x < 0}\\ undetermined, & \text {if x = 0 ... eq.(2.4)} \end{cases} $$ Let us assume that \(x \ne 0\). When \(x=0\) there are several ways of dealing with it, including using a slightly modified ReLu function but that is outside the scope of this article. Let's now look at the two cases with \(x=c_{10}\),

Case 1: \(x \lt 0\),
In eq.(2.2),
$$
\begin{align}
{\partial (max(0,c_{10})) \over \partial w_{00}^1}&={\partial 0\over \partial w_{00}^1} \text { (from eq.(2.4))}\\
&=0\text{ ... eq.(2.5)}
\end{align}
$$
Case 2: \(x \gt 0\),
In eq.(2.2),
$$
\begin{align}
{\partial (max(0,c_{10})) \over \partial w_{00}^1}&={\partial c_{10}\over \partial w_{00}^1} \text { (from eq.(2.4))} \text{ ... eq.(2.6)}\\
\end{align}
$$
Solving for eq.(2.6),
$$
\begin{align}
{\partial c_{10}\over \partial w_{00}^1}&={\partial {(u_{10}^1.w_{11} + u_{20}^1.w_{01}+u_{11}^1.w_{10}+
u_{21}^1.w_{00})}\over \partial w_{00}^1} \text { (substituting full value of } c_{10} \text{)}\\
&={\partial {(u_{10}^1.w_{11})} \over \partial w_{00}^1}+ {\partial {(u_{20}^1.w_{01})} \over \partial w_{00}^1} + {\partial {(u_{11}^1.w_{10})} \over \partial w_{00}^1} + {\partial {(u_{21}^1.w_{00})} \over \partial w_{00}^1} \\
&={\partial {(max(c_{10}^1,0).w_{11})} \over \partial w_{00}^1}+ {\partial {(max(c_{20}^1,0).w_{01})} \over \partial w_{00}^1} + {\partial {(max(c_{11}^1,0).w_{10})} \over \partial w_{00}^1} +
{\partial {(max(c_{21}^1,0).w_{00})} \over \partial w_{00}^1}\\
&=w_{11}.{\partial {(max(c_{10}^1,0))} \over \partial w_{00}^1}+ w_{01}.{\partial {(max(c_{20}^1,0))} \over \partial w_{00}^1} + w_{10}.{\partial {(max(c_{11}^1,0))} \over \partial w_{00}^1} +
w_{00}.{\partial {(max(c_{21}^1,0))} \over \partial w_{00}^1} \text{ ... eq.(2.7)}\\
\end{align}
$$
We will now have to expand the values of \(c_{10}^1\) through \(c_{21}^1\). These values are given as:

---

$$
\begin{align}
c_{10}^1&=i_{10}.w_{11}^1 + i_{20}.w_{01}^1+i_{11}.w_{10}^1 + i_{21}.w_{00}^1\\
c_{20}^1&=i_{20}.w_{11}^1 + i_{30}.w_{01}^1+i_{21}.w_{10}^1 + i_{31}.w_{00}^1\\
c_{11}^1&=i_{11}.w_{11}^1 + i_{21}.w_{01}^1+i_{12}.w_{10}^1 + i_{22}.w_{00}^1\\
c_{21}^1&=i_{21}.w_{11}^1 + i_{31}.w_{01}^1+i_{22}.w_{10}^1 + i_{32}.w_{00}^1\\
\end{align}
$$

---

Let us now find the partial derivative of each individual term in eq. (2.7), starting with \(w_{11}.{\partial {(max(c_{10}^1,0))} \over \partial w_{00}^1}\). There will be 2 cases depending on value of \(c_{10}^1\). We will not consider the case when \(c_{10}^1=0\).

Case 1: \(c_{10}^1 \lt 0\),

$$
\begin{align}
w_{11}.{\partial {(max(c_{10}^1,0))} \over \partial w_{00}^1}&=w_{11}.{\partial 0 \over \partial w_{00}^1} \text { (as,} max(c_{10}^1,0)=0 \text {)}\\
&=0 \text { ...eq.(2.7.1.1)}
\end{align}
$$

Case 2: \(c_{10}^1 \gt 0\),

$$
\begin{align}
w_{11}.{\partial {(max(c_{10}^1,0))} \over \partial w_{00}^1}&=w_{11}.{\partial {(i_{10}.w_{11}^1 + i_{20}.w_{01}^1+i_{11}.w_{10}^1 + i_{21}.w_{00}^1)} \over \partial w_{00}^1} \\
&\text { (as,} max(c_{10}^1,0)=c_{10}^1 \text {, putting full value of } c_{10}^1 \text {)}\\
&=w_{11}.{{\partial {(i_{10}.w_{11}^1)} \over \partial w_{00}^1} +
{\partial {(i_{20}.w_{01}^1)} \over \partial w_{00}^1} +
{\partial {(i_{11}.w_{10}^1)} \over \partial w_{00}^1} +
{\partial {(i_{21}.w_{00}^1)} \over \partial w_{00}^1}} \\
&=w_{11}.{{0} + {0} + {0} + i_{21}}\\
&=w_{11}.i_{21} \text { ...eq.(2.7.1.2)}\\
\end{align}
$$
Let us now find \(w_{01}.{\partial {(max(c_{20}^1,0))} \over \partial w_{00}^1}\), with the 2 cases.We will not consider the case when \(c_{20}^1=0\).

Case 1: \(c_{20}^1 \lt 0\),

$$
\begin{align}
w_{01}.{\partial {(max(c_{20}^1,0))} \over \partial w_{00}^1}&=w_{11}.{\partial 0 \over \partial w_{00}^1} \text { (as,} max(c_{20}^1,0)=0 \text {)}\\
&=0 \text { ...eq.(2.7.2.1)}
\end{align}
$$

Case 2: \(c_{20}^1 \gt 0\),

$$
\begin{align}
w_{01}.{\partial {(max(c_{20}^1,0))} \over \partial w_{00}^1}&=w_{01}.{\partial {(i_{20}.w_{11}^1 + i_{30}.w_{01}^1+i_{21}.w_{10}^1 + i_{31}.w_{00}^1)} \over \partial w_{00}^1} \\
&\text { (as,} max(c_{20}^1,0)=c_{20}^1 \text {, putting full value of } c_{20}^1 \text {)}\\
&=w_{01}.{{\partial {(i_{20}.w_{11}^1)} \over \partial w_{00}^1} +
{\partial {(i_{30}.w_{01}^1)} \over \partial w_{00}^1} +
{\partial {(i_{21}.w_{10}^1)} \over \partial w_{00}^1} +
{\partial {(i_{31}.w_{00}^1)} \over \partial w_{00}^1}}\\
&=w_{01}.{{0} + {0} + {0} + i_{31}}\\
&=w_{01}.i_{31} \text { ...eq.(2.7.2.2)}\\
\end{align}
$$
Let us now find \(w_{10}.{\partial {(max(c_{11}^1,0))} \over \partial w_{00}^1}\), with the 2 cases. We will not consider the case when \(c_{11}^1=0\).

Case 1: \(c_{11}^1 \lt 0\),

$$
\begin{align}
w_{10}.{\partial {(max(c_{11}^1,0))} \over \partial w_{00}^1}&=w_{10}.{\partial 0 \over \partial w_{00}^1} \text { (as,} max(c_{11}^1,0)=0 \text {)}\\
&=0 \text { ...eq.(2.7.3.1)}
\end{align}
$$

Case 2: \(c_{11}^1 \gt 0\),

$$
\begin{align}
w_{10}.{\partial {(max(c_{11}^1,0))} \over \partial w_{00}^1}&=w_{10}.{\partial {(i_{11}.w_{11}^1 + i_{21}.w_{01}^1+i_{12}.w_{10}^1 + i_{22}.w_{00}^1)} \over \partial w_{00}^1} \\
&\text { (as,} max(c_{11}^1,0)=c_{11}^1 \text {, putting full value of } c_{11}^1 \text {)}\\
&=w_{10}.{{\partial {(i_{11}.w_{11}^1)} \over \partial w_{00}^1} +
{\partial {(i_{21}.w_{01}^1)} \over \partial w_{00}^1} +
{\partial {(i_{12}.w_{10}^1)} \over \partial w_{00}^1} +
{\partial {(i_{22}.w_{00}^1)} \over \partial w_{00}^1}}\\
&=w_{10}.{{0} + {0} + {0} + i_{22}}\\
&=w_{10}.i_{22} \text { ...eq.(2.7.3.2)}\\
\end{align}
$$
Finally, let us find \(w_{00}.{\partial {(max(c_{21}^1,0))} \over \partial w_{00}^1}\), with the 2 cases. We will not consider the case when \(c_{21}^1=0\).

Case 1: \(c_{21}^1 \lt 0\),

$$
\begin{align}
w_{00}.{\partial {(max(c_{21}^1,0))} \over \partial w_{00}^1}&=w_{00}.{\partial 0 \over \partial w_{00}^1} \text { (as,} max(c_{11}^1,0)=0 \text {)}\\
&=0 \text { ...eq.(2.7.4.1)}
\end{align}
$$

Case 2: \(c_{21}^1 \gt 0\),

$$
\begin{align}
w_{00}.{\partial {(max(c_{21}^1,0))} \over \partial w_{00}^1}&=w_{00}.{\partial {(i_{21}.w_{11}^1 + i_{31}.w_{01}^1+i_{22}.w_{10}^1 + i_{32}.w_{00}^1)} \over \partial w_{00}^1} \\
&\text { (as,} max(c_{21}^1,0)=c_{21}^1 \text {, putting full value of } c_{21}^1 \text {)}\\
&=w_{00}.{{\partial {(i_{21}.w_{11}^1)} \over \partial w_{00}^1} +
{\partial {(i_{31}.w_{01}^1)} \over \partial w_{00}^1} +
{\partial {(i_{22}.w_{10}^1)} \over \partial w_{00}^1} +
{\partial {(i_{32}.w_{00}^1)} \over \partial w_{00}^1}} \\
&=w_{00}.{{0} + {0} + {0} + i_{32}}\\
&=w_{00}.i_{32} \text { ...eq.(2.7.4.2)}\\
\end{align}
$$
Putting the values of eqs.(2.7.x.x) in eq. (2.7),
$$
\begin{align}
{\partial c_{10}\over \partial w_{00}^1}=&w_{11}.{\partial {(max(c_{10}^1,0))} \over \partial w_{00}^1}+ w_{01}.{\partial {(max(c_{20}^1,0))} \over \partial w_{00}^1} + w_{10}.{\partial {(max(c_{11}^1,0))} \over \partial w_{00}^1} + w_{00}.{\partial {(max(c_{21}^1,0))} \over \partial w_{00}^1}\\
&\text{ (from eq.(2.7))}\\
{\partial c_{10}\over \partial w_{00}^1}=&w_{11}.i_{21}+ w_{01}.i_{31} + w_{10}.i_{22} + w_{00}.i_{32} \text{ (from eqs.(2.7.x.x)) ... eq.(2.8)}\\
\end{align}
$$
Note that eq.(2.8) assumes that \(c_{10}^1,c_{20}^1,c_{11}^1,c_{21}^1\) are all \(\gt 0\). If any of \(c_{10}^1,c_{20}^1,c_{11}^1,c_{21}^1\) are \(\lt 0\), then the corresponding multiple term (\(i_{21},i_{31},i_{22},i_{32}\)) should be made 0.

Generic form of eq.(2.7),
$$
\begin{align}
{\partial c_{10}\over \partial w_{00}^1}=&w_{11}.{\partial {(max(c_{10}^1,0))} \over \partial w_{00}^1}+ w_{01}.{\partial {(max(c_{20}^1,0))} \over \partial w_{00}^1} + w_{10}.{\partial {(max(c_{11}^1,0))} \over \partial w_{00}^1} + w_{00}.{\partial {(max(c_{21}^1,0))} \over \partial w_{00}^1}\\
&\text{ (from eq.(2.7))}\\
=&w_{11}.{\partial u_{10}^1 \over \partial w_{00}^1}+ w_{01}.{\partial u_{20}^1 \over \partial w_{00}^1} + w_{10}.{\partial u_{11}^1 \over \partial w_{00}^1} + w_{00}.{\partial u_{21}^1 \over \partial w_{00}^1}\\
=&w_{11}.{\partial f(c_{10}^1) \over \partial w_{00}^1}+ w_{01}.{\partial f(c_{20}^1) \over \partial w_{00}^1} + w_{10}.{\partial f(c_{11}^1) \over \partial w_{00}^1} + w_{00}.{\partial f(u_{21}^1) \over \partial w_{00}^1} \text {... eq.(2.9)}\\
&\text {where,} f(c_{xy}^1) \text { is the activation function (like ReLu etc.)}\\
\end{align}
$$
Going back to eq.(2.1),
$$
\begin{align}
{\partial E \over \partial w_{00}^1}&={\partial E \over \partial u_{10}}.{\partial u_{10} \over \partial w_{00}^1} \text{ ... eq.(2.1)}\\
\end{align}
$$
Let us now solve for the left term of eq.(2.1), which is \({\partial E \over \partial u_{10}}\),

---

$$
\begin{align}
{\partial E \over \partial u_{10}}&={\partial {(t - r_{fc})^2\over 2} \over \partial u_{10}} \text { (putting value of E)}\\
&={1 \over 2}.{\partial {(t - r_{fc})^2} \over \partial u_{10}}
\end{align}
$$
Applying the chain rule to the above equation:
$$
\text{Here, } z = {t - r_{fc}},x=z^2, \text{ and } y=u_{10} \text{ ,therefore, }\\
\begin{align}
{1 \over 2}.{\partial {(t - r_{fc})^2}\over \partial u_{10}}&={1 \over 2}.{\partial x\over \partial y}\\
&={1 \over 2}.{\partial x\over \partial z}.{\partial z\over \partial y}\\
&={1 \over 2}.{\partial z^2\over \partial z}.{\partial z\over \partial y}\\
&={1 \over 2}.{\partial (t - r_{fc})^2\over \partial (t - r_{fc})}.{\partial (t - r_{fc})\over \partial u_{10}}\\
&={1 \over 2}.{2(t - r_{fc})}.{\partial (t - r_{fc})\over \partial u_{10}} \text{ ... eq.(2.1.1)}\\
\end{align}
$$
Further,
$$
\begin{align}
{\partial (t - r_{fc})\over \partial u_{10}}&={\partial (t - w_{fc}.r_p)\over \partial u_{10}}\\
&={\partial t\over \partial u_{10}} - {\partial w_{fc}.r_p\over \partial u_{10}}\\
&={\partial t\over \partial u_{10}} - w_{fc}.{\partial r_p\over \partial u_{10}}\\
&={\partial t\over \partial u_{10}} - w_{fc}.{\partial u_{10}\over \partial u_{10}} \text { as,(} r_[ = u_{10} \text {)}\\
&=0 - w_{fc} \text{ (as,} {\partial C \over \partial x}=0 \text { and } {\partial x \over \partial x}=1, \text {where C is a constant)}, \text{ ... eq.(2.1.2)}\\
\end{align}
$$
Applying eq.(2.1.2) in eq.(2.1.1),
$$
\begin{align}
{1 \over 2}.{\partial {(t - r_{fc})^2}\over \partial u_{10}}&={1 \over 2}.{2(t - r_{fc})}.{\partial (t - r_{fc})\over \partial u_{10}}\\
&={1 \over 2}.{2(t - r_{fc})}.{(0 - w_{fc})}\\
&=(t - r_{fc}).(-w_{fc})\\
&=-(t - r_{fc}).w_{fc}\\
\end{align}
$$

---

Therefore,
$$
\begin{align}
\partial E\over \partial u_{10}&={\partial {(t - r_{fc})^2\over 2}\over \partial u_{10}}\\
&={1 \over 2}.{\partial {(t - r_{fc})^2}\over \partial u_{10}} \\
&=-(t - r_{fc}).w_{fc} \text{ ... eq.(2.1.3)}\\
\end{align}
$$
Putting values of eqs.(2.1.3) and (2.9) in eq.(2.1),
$$
\begin{align}
{\partial E \over \partial w_{00}^1}&={\partial E \over \partial u_{10}}.{\partial u_{10} \over \partial w_{00}^1} \text {(from eq.(2.1))}\\
&=-(t - r_{fc}).w_{fc}.{\partial u_{10} \over \partial w_{00}^1} \text { (putting value from eq.(2.1.3)) ... eq.(2.10)} \\
&=-(t - r_{fc}).w_{fc}.{(w_{11}.{\partial f(c_{10}^1) \over \partial w_{00}^1}+ w_{01}.{\partial f(c_{20}^1) \over \partial w_{00}^1} + w_{10}.{\partial f(c_{11}^1) \over \partial w_{00}^1} + w_{00}.{\partial f(u_{21}^1) \over \partial w_{00}^1})} \text { ...eq.(2.11)}\\
&\text { (as,}{\partial u_{10} \over \partial w_{00}^1}={\partial c_{10} \over \partial w_{00}^1} \text{
if } c_{10} > 0 \text{, and putting value of } {\partial c_{10} \over \partial w_{00}^1} \text {from eq.(2.9))}\\
\end{align}
$$
Let us now compute \({\partial E \over \partial w_{10}^1}\), and after that we will come up with a generic form to derive \({\partial E \over \partial w_{01}^1}\) and \({\partial E \over \partial w_{11}^1}\),

Applying the chain rule,
$$
\begin{align}
{\partial x \over \partial y}&={\partial x\over \partial z}.{\partial z\over \partial y}\\
\text{Here, } z = u_{10}, x&=E, \text{ and } y=w_{10}^1 \text{ ,therefore, }\\
{\partial E \over \partial w_{10}^1}&={\partial E \over \partial u_{10}}.{\partial u_{10} \over \partial w_{10}^1} \text{ ... eq.(3.1)}\\
\end{align}
$$
Solving for the right term \({\partial u_{10} \over \partial w_{10}^1}\) in eq.(3.1):
$$
\begin{align}
{\partial u_{10} \over \partial w_{10}^1}&={\partial (max(0,c_{10})) \over \partial w_{10}^1} \text{ ... eq.(3.2)}
\end{align}
$$
Now,
$$
{d {{max(0,x)} \over {dx}}}=
\begin{cases}
x, & \text {if x > 0}\\
0, & \text {if x < 0}\\ undetermined, & \text {if x = 0 ... eq.(3.4)} \end{cases} $$ Let us assume that \(x \ne 0\). When \(x=0\) there are several ways of dealing with it, including using a slightly modified ReLu function but that is outside the scope of this article. Let's now look at the two cases with \(x=c_{10}\),

Case 1: \(x \lt 0\),
In eq.(3.2),
$$
\begin{align}
{\partial (max(0,c_{10})) \over \partial w_{10}^1}&={\partial 0\over \partial w_{10}^1} \text { (from eq.(3.4))}\\
&=0\text{ ... eq.(3.5)}
\end{align}
$$
Case 2: \(x \gt 0\),
In eq.(3.2),
$$
\begin{align}
{\partial (max(0,c_{10})) \over \partial w_{00}^1}&={\partial c_{10}\over \partial w_{00}^1} \text { (from eq.(3.4))} \text{ ... eq.(3.6)}\\
\end{align}
$$
Solving for eq.(3.6),
$$
\begin{align}
{\partial c_{10}\over \partial w_{10}^1}&={\partial {(u_{10}^1.w_{11} + u_{20}^1.w_{01}+u_{11}^1.w_{10}+
u_{21}^1.w_{00})}\over \partial w_{10}^1} \text { (substituting full value of } c_{10} \text{)}\\
&={\partial {(u_{10}^1.w_{11})} \over \partial w_{10}^1}+ {\partial {(u_{20}^1.w_{01})} \over \partial w_{10}^1} + {\partial {(u_{11}^1.w_{10})} \over \partial w_{10}^1} + {\partial {(u_{21}^1.w_{00})} \over \partial w_{10}^1} \\
&={\partial {(max(c_{10}^1,0).w_{11})} \over \partial w_{10}^1}+ {\partial {(max(c_{20}^1,0).w_{01})} \over \partial w_{10}^1} + {\partial {(max(c_{11}^1,0).w_{10})} \over \partial w_{10}^1} +
{\partial {(max(c_{21}^1,0).w_{00})} \over \partial w_{10}^1}\\
&=w_{11}.{\partial {(max(c_{10}^1,0))} \over \partial w_{10}^1}+ w_{01}.{\partial {(max(c_{20}^1,0))} \over \partial w_{10}^1} + w_{10}.{\partial {(max(c_{11}^1,0))} \over \partial w_{10}^1} +
w_{00}.{\partial {(max(c_{21}^1,0))} \over \partial w_{10}^1} \text{ ... eq.(3.7)}\\
\end{align}
$$
We already know the expanded values of \(c_{10}^1\) through \(c_{21}^1\). Let us now find the partial derivative of each individual term in eq.(3.7), starting with \(w_{11}.{\partial {(max(c_{10}^1,0))} \over \partial w_{10}^1}\). There will be 2 cases depending on value of \(c_{10}^1\). We will not consider the case when \(c_{10}^1=0\).

Case 1: \(c_{10}^1 \lt 0\),

$$
\begin{align}
w_{11}.{\partial {(max(c_{10}^1,0))} \over \partial w_{00}^1}&=w_{11}.{\partial 0 \over \partial w_{00}^1} \text { (as,} max(c_{10}^1,0)=0 \text {)}\\
&=0 \text { ...eq.(3.7.1.1)}
\end{align}
$$

Case 2: \(c_{10}^1 \gt 0\),

$$
\begin{align}
w_{11}.{\partial {(max(c_{10}^1,0))} \over \partial w_{00}^1}&=w_{11}.{\partial {(i_{10}.w_{11}^1 + i_{20}.w_{01}^1+i_{11}.w_{10}^1 + i_{21}.w_{00}^1)} \over \partial w_{10}^1} \\
&\text { (as,} max(c_{10}^1,0)=c_{10}^1 \text {, putting full value of } c_{10}^1 \text {)}\\
&=w_{11}.{{\partial {(i_{10}.w_{11}^1)} \over \partial w_{10}^1} +
{\partial {(i_{20}.w_{01}^1)} \over \partial w_{10}^1} +
{\partial {(i_{11}.w_{10}^1)} \over \partial w_{10}^1} +
{\partial {(i_{21}.w_{00}^1)} \over \partial w_{10}^1}} \\
&=w_{11}.{{0} + {0} + i_{11} + 0}\\
&=w_{11}.i_{11} \text { ...eq.(3.7.1.2)}\\
\end{align}
$$
Let us now find \(w_{01}.{\partial {(max(c_{20}^1,0))} \over \partial w_{10}^1}\), with the 2 cases. We will not consider the case when \(c_{20}^1=0\).

Case 1: \(c_{20}^1 \lt 0\),

$$
\begin{align}
w_{01}.{\partial {(max(c_{20}^1,0))} \over \partial w_{10}^1}&=w_{11}.{\partial 0 \over \partial w_{10}^1} \text { (as,} max(c_{20}^1,0)=0 \text {)}\\
&=0 \text { ...eq.(3.7.2.1)}
\end{align}
$$

Case 2: \(c_{20}^1 \gt 0\),

$$
\begin{align}
w_{01}.{\partial {(max(c_{20}^1,0))} \over \partial w_{10}^1}&=w_{01}.{\partial {(i_{20}.w_{11}^1 + i_{30}.w_{01}^1+i_{21}.w_{10}^1 + i_{31}.w_{00}^1)} \over \partial w_{10}^1} \\
&\text { (as,} max(c_{20}^1,0)=c_{20}^1 \text {, putting full value of } c_{20}^1 \text {)}\\
&=w_{01}.{{\partial {(i_{20}.w_{11}^1)} \over \partial w_{10}^1} +
{\partial {(i_{30}.w_{01}^1)} \over \partial w_{10}^1} +
{\partial {(i_{21}.w_{10}^1)} \over \partial w_{10}^1} +
{\partial {(i_{31}.w_{00}^1)} \over \partial w_{10}^1}}\\
&=w_{01}.{{0} + {0} + i_{21} + 0}\\
&=w_{01}.i_{21} \text { ...eq.(3.7.2.2)}\\
\end{align}
$$
Let us now find \(w_{10}.{\partial {(max(c_{11}^1,0))} \over \partial w_{10}^1}\), with the 2 cases. We will not consider the case when \(c_{11}^1=0\).

Case 1: \(c_{11}^1 \lt 0\),

$$
\begin{align}
w_{10}.{\partial {(max(c_{11}^1,0))} \over \partial w_{10}^1}&=w_{10}.{\partial 0 \over \partial w_{10}^1} \text { (as,} max(c_{11}^1,0)=0 \text {)}\\
&=0 \text { ...eq.(3.7.3.1)}
\end{align}
$$

Case 2: \(c_{11}^1 \gt 0\),

$$
\begin{align}
w_{10}.{\partial {(max(c_{11}^1,0))} \over \partial w_{00}^1}&=w_{10}.{\partial {(i_{11}.w_{11}^1 + i_{21}.w_{01}^1+i_{12}.w_{10}^1 + i_{22}.w_{00}^1)} \over \partial w_{10}^1} \\
&\text { (as,} max(c_{11}^1,0)=c_{11}^1 \text {, putting full value of } c_{11}^1 \text {)}\\
&=w_{10}.{{\partial {(i_{11}.w_{11}^1)} \over \partial w_{10}^1} +
{\partial {(i_{21}.w_{01}^1)} \over \partial w_{10}^1} +
{\partial {(i_{12}.w_{10}^1)} \over \partial w_{10}^1} +
{\partial {(i_{22}.w_{00}^1)} \over \partial w_{10}^1}}\\
&=w_{10}.{{0} + {0} + i_{12} + {0}}\\
&=w_{10}.i_{12} \text { ...eq.(3.7.3.2)}\\
\end{align}
$$
Finally, let us find \(w_{00}.{\partial {(max(c_{21}^1,0))} \over \partial w_{10}^1}\), with the 2 cases. We will not consider the case when \(c_{21}^1=0\).

Case 1: \(c_{21}^1 \lt 0\),

$$
\begin{align}
w_{00}.{\partial {(max(c_{21}^1,0))} \over \partial w_{10}^1}&=w_{00}.{\partial 0 \over \partial w_{10}^1} \text { (as,} max(c_{11}^1,0)=0 \text {)}\\
&=0 \text { ...eq.(3.7.4.1)}
\end{align}
$$

Case 2: \(c_{21}^1 \gt 0\),

$$
\begin{align}
w_{00}.{\partial {(max(c_{21}^1,0))} \over \partial w_{10}^1}&=w_{00}.{\partial {(i_{21}.w_{11}^1 + i_{31}.w_{01}^1+i_{22}.w_{10}^1 + i_{32}.w_{00}^1)} \over \partial w_{10}^1} \\
&\text { (as,} max(c_{21}^1,0)=c_{21}^1 \text {, putting full value of } c_{21}^1 \text {)}\\
&=w_{00}.{{\partial {(i_{21}.w_{11}^1)} \over \partial w_{10}^1} +
{\partial {(i_{31}.w_{01}^1)} \over \partial w_{10}^1} +
{\partial {(i_{22}.w_{10}^1)} \over \partial w_{10}^1} +
{\partial {(i_{32}.w_{00}^1)} \over \partial w_{10}^1}} \\
&=w_{00}.{{0} + {0} + i_{22} + {0}}\\
&=w_{00}.i_{22} \text { ...eq.(3.7.4.2)}\\
\end{align}
$$
Putting the values of eqs.(3.7.x.x) in eq. (3.7),
$$
\begin{align}
{\partial c_{10}\over \partial w_{10}^1}&=w_{11}.{\partial {(max(c_{10}^1,0))} \over \partial w_{10}^1}+ w_{01}.{\partial {(max(c_{20}^1,0))} \over \partial w_{10}^1} + w_{10}.{\partial {(max(c_{11}^1,0))} \over \partial w_{10}^1} + w_{00}.{\partial {(max(c_{21}^1,0))} \over \partial w_{10}^1}\\
&\text{ (from eq.(3.7))}\\
{\partial c_{10}\over \partial w_{10}^1}&=w_{11}.i_{11} + w_{01}.i_{21} + w_{10}.i_{12} + w_{00}.i_{22}
\text{ (from eqs.(3.7.x.x)) ... eq.(3.8)}\\
\end{align}
$$
Note that eq.(3.8) assumes that \(c_{10}^1,c_{20}^1,c_{11}^1,c_{21}^1\) are all \(\gt 0\). If any of \(c_{10}^1,c_{20}^1,c_{11}^1,c_{21}^1\) are \(\lt 0\), then the corresponding multiple term (\(i_{21},i_{31},i_{22},i_{32})\) should be made 0.

Generic form of eq.(3.7),
$$
\begin{align}
{\partial c_{10}\over \partial w_{10}^1}=&w_{11}.{\partial {(max(c_{10}^1,0))} \over \partial w_{10}^1}+ w_{01}.{\partial {(max(c_{20}^1,0))} \over \partial w_{10}^1} + w_{10}.{\partial {(max(c_{11}^1,0))} \over \partial w_{10}^1} + w_{00}.{\partial {(max(c_{21}^1,0))} \over \partial w_{10}^1}\\
&\text{ (from eq.(3.7))}\\
=&w_{11}.{\partial u_{10}^1 \over \partial w_{10}^1}+ w_{01}.{\partial u_{20}^1 \over \partial w_{10}^1} + w_{10}.{\partial u_{11}^1 \over \partial w_{10}^1} + w_{00}.{\partial u_{21}^1 \over \partial w_{10}^1}\\
=&w_{11}.{\partial f(c_{10}^1) \over \partial w_{10}^1}+ w_{01}.{\partial f(c_{20}^1) \over \partial w_{10}^1} + w_{10}.{\partial f(c_{11}^1) \over \partial w_{10}^1} + w_{00}.{\partial f(c_{21}^1) \over \partial w_{10}^1} \text {... eq.(3.9)}\\
&\text {where,} f(c_{xy}^1) \text { is the activation function (like ReLu etc.)}\\
\end{align}
$$
Going back to eq.(3.1), we can use the same derivation as we used in eq.(2.1.3) as the term \(\partial E\over \partial u_{10}\) is the same.
$$
\begin{align}
\partial E\over \partial u_{10}&={\partial {(t - r_{fc})^2\over 2}\over \partial u_{10}} \text{(from eq.(2.1.3))}\\
&={1 \over 2}.{\partial {(t - r_{fc})^2}\over \partial u_{10}} \\
&=-(t - r_{fc}).w_{fc} \text{ ... eq.(3.1.3)}\\
\end{align}
$$
Putting values of eqs.(3.1.3) and (3.9) in eq.(3.1),
$$
\begin{align}
{\partial E \over \partial w_{10}^1}&={\partial E \over \partial u_{10}}.{\partial u_{10} \over \partial w_{10}^1} \\
&=-(t - r_{fc}).w_{fc}.{\partial u_{10} \over \partial w_{10}^1} \text { (putting value from eq.(3.1.3)) ... eq.(3.10)} \\
&=-(t - r_{fc}).w_{fc}.{(w_{11}.{\partial f(c_{10}^1) \over \partial w_{10}^1}+ w_{01}.{\partial f(c_{20}^1) \over \partial w_{10}^1} + w_{10}.{\partial f(c_{11}^1) \over \partial w_{10}^1} + w_{00}.{\partial f(c_{21}^1) \over \partial w_{10}^1})} \text { ... eq.(3.11)}\\
&\text { (putting value from eq.(3.9))}\\
\end{align}
$$
We will now come up with a general form based on which we will derive \({\partial E \over \partial w_{01}^1}\) and \({\partial E \over \partial w_{11}^1}\).

General form:
Listing eqs.(2.11) and (3.11),
$$
\begin{align}
{\partial E \over \partial w_{00}^1}&=-(t - r_{fc}).w_{fc}.{(w_{11}.{\partial f(c_{10}^1) \over \partial w_{00}^1}+ w_{01}.{\partial f(c_{20}^1) \over \partial w_{00}^1} + w_{10}.{\partial f(c_{11}^1) \over \partial w_{00}^1} + w_{00}.{\partial f(u_{21}^1) \over \partial w_{00}^1})} \text { (from eq.(2.11))}\\
{\partial E \over \partial w_{10}^1}&=-(t - r_{fc}).w_{fc}.{(w_{11}.{\partial f(c_{10}^1) \over \partial w_{10}^1}+ w_{01}.{\partial f(c_{20}^1) \over \partial w_{10}^1} + w_{10}.{\partial f(c_{11}^1) \over \partial w_{10}^1} + w_{00}.{\partial f(c_{21}^1) \over \partial w_{10}^1})} \text { (from eq.(3.11))}\\
\end{align}
$$
From these equations, it is clear that the only term different between them is \({\partial f(c_{xy}^1) \over \partial w_{10}^1}\). Hence a generic form of eqs.(2.11) and (3.11) can be derived if \({\partial f(c_{xy}^1) \over \partial w_{10}^1}\) is made generic.

Therefore the generic form of eqs.(2.11) and eqs.(3.11) is,
$$
\begin{align}
{\partial E \over \partial w_{xy}^1}&=-(t - r_{fc}).w_{fc}.{(w_{11}.{\partial f(c_{10}^1) \over \partial w_{xy}^1}+ w_{01}.{\partial f(c_{20}^1) \over \partial w_{xy}^1} + w_{10}.{\partial f(c_{11}^1) \over \partial w_{xy}^1} + w_{00}.{\partial f(c_{21}^1) \over \partial w_{xy}^1})} \text { ... eq.(4.1)}\\
&\text {(where,} f(c_{xy}^1) \text { is the activation function (like ReLu etc.))}
\end{align}
$$
Let us look at eqs.(2.8) and (3.8) to come up with a generic form when the activation function is ReLu,
$$
\begin{align}
{\partial c_{10}\over \partial w_{00}^1}&=w_{11}.i_{21}+ w_{01}.i_{31} + w_{10}.i_{22} + w_{00}.i_{32} \text{ (from eq.(2.8))}\\
{\partial c_{10}\over \partial w_{10}^1}&=w_{11}.i_{11} + w_{01}.i_{21} + w_{10}.i_{12} + w_{00}.i_{22}
\text{ (from eq.(3.8))}\\
\end{align}
$$
Intuitively we can see that the downstream weights \(w_{11}\) through \(w_{00}\) are multiplied with input values that the upstream weights \(w_{00}^1\) and \(w_{01}^1\) are multiplied with.

Consider the following CNN diagram which highlights (in brown) all inputs values that will be multiplied with \(w_{00}^1\) as the 2x2 filter is slided over the 4x4 input with a stride of 1 as the convolution operation is performed. Remember that as shown in part-I, when doing the convolution operation, we have to invert the filter matrix before doing the multiplication (dot product).

The following diagram shows how the same input values (which are multiplied by \(w_{00}^1\)) are multiplied by the downstream filter values to give us \({\partial c_{10}\over \partial w_{00}^1} = w_{11}.i_{21}+ w_{01}.i_{31} + w_{10}.i_{22} + w_{00}.i_{32}\). The matching colors between each element of the downstream filter matrix and the input matrix show which elements are multiplied.

Now consider the following CNN diagram that highlights (in brown) all inputs values that will be multiplied with \(w_{10}^1\).

The following diagram shows how the same input values (which are multiplied by \(w_{10}^1\)) are multiplied by the downstream filter values to give us \({\partial c_{10}\over \partial w_{10}^1}=w_{11}.i_{11} + w_{01}.i_{21} + w_{10}.i_{12} + w_{00}.i_{22}\).

Let us extrapolate the pattern to find \({\partial c_{10}\over \partial w_{01}^1}\)

Now consider the following CNN diagram that highlights (in brown) all inputs values that will be multiplied with \(w_{01}^1\),

The following diagram shows how the same input values (which are multiplied by \(w_{01}^1\)) are multiplied by the downstream filter values to give us \({\partial c_{10}\over \partial w_{01}^1}=w_{11}.i_{20} + w_{01}.i_{30} + w_{10}.i_{21} + w_{00}.i_{31}\).

Similarly for \({\partial c_{10}\over \partial w_{11}^1}\), consider the following CNN diagram that highlights (in brown) all inputs values that will be multiplied with \(w_{11}^1\),

The following diagram shows how the same input values (which are multiplied by \(w_{11}^1\)) are multiplied by the downstream filter values to give us \({\partial c_{10}\over \partial w_{11}^1}=w_{11}.i_{10} + w_{01}.i_{20} + w_{10}.i_{11} + w_{00}.i_{21}\).

Listing values of \({\partial c_{10}\over \partial w_{00}^1},{\partial c_{10}\over \partial w_{01}^1},{\partial c_{10}\over \partial w_{10}^1},{\partial c_{10}\over \partial w_{11}^1}\), together,

$$
\begin{align}
{\partial c_{10}\over \partial w_{00}^1}&=w_{11}.i_{21}+ w_{01}.i_{31} + w_{10}.i_{22} + w_{00}.i_{32} \\
{\partial c_{10}\over \partial w_{10}^1}&=w_{11}.i_{11} + w_{01}.i_{21} + w_{10}.i_{12} + w_{00}.i_{22}\\
{\partial c_{10}\over \partial w_{01}^1}&=w_{11}.i_{20} + w_{01}.i_{30} + w_{10}.i_{21} + w_{00}.i_{31}\\
{\partial c_{10}\over \partial w_{11}^1}&=w_{11}.i_{10} + w_{01}.i_{20} + w_{10}.i_{11} + w_{00}.i_{21}\\
\end{align}
$$
An unpure generic form of the above equations is,
$$
\begin{align}
{\partial c_{10}\over \partial w_{xy}^1}&=\sum_{a=0,b=0}^{a=n,b=n} {w_{ab}.i_{pq}} \text { ... eq.(4.2)}\\
&\text {(Here, } w_{ab} \text{ represents all filter values of the downstream layer, and }\\
&i_{pq} \text { is an element of the input matrix that is composed of elements that will be multiplied by } w_{xy}^1.\\
&n+1\text{ is the size of downstream filter matrix)}
\end{align}
$$
Listing eqs.(2.10) and (3.10)
$$
\begin{align}
{\partial E \over \partial w_{00}^1}&=-(t - r_{fc}).w_{fc}.{\partial u_{10} \over \partial w_{00}^1} \text{ (from (eq.(2.10))}\\
{\partial E \over \partial w_{10}^1}&=-(t - r_{fc}).w_{fc}.{\partial u_{10} \over \partial w_{10}^1} \text { (from eq.(3.10))}
\end{align}
$$
Now since the activation function is ReLu, \(u_{10} = max(c_{10},0)\), and assuming \(c_{10}>0\), eqs.(2.10) and (3.10) can be re-written as,
$$
\begin{align}
{\partial E \over \partial w_{00}^1}&=-(t - r_{fc}).w_{fc}.{\partial c_{10} \over \partial w_{00}^1} \text{ (from (eq.(2.10))}\\
{\partial E \over \partial w_{10}^1}&=-(t - r_{fc}).w_{fc}.{\partial c_{10} \over \partial w_{10}^1} \text { (from eq.(3.10))}
\end{align}
$$
Or a more generic form,
$$
\begin{align}
{\partial E \over \partial w_{xy}^1}&=-(t - r_{fc}).w_{fc}.{\partial c_{10} \over \partial w_{xy}^1} \text { ... eq.(4.3)}\\
{\partial E \over \partial w_{xy}^1}&=-(t - r_{fc}).w_{fc}.\sum_{a=0,b=0}^{a=n,b=n} {w_{ab}.i_{pq}} \text { (from eq.(4.2)) ... eq.(4.4)}\\
\end{align}
$$
After backpropagation, each weight \(w_{xy}^1\) will be updated as,
$$
\begin{align}
\Delta w_{xy}^1&=-\eta.{\partial E\over \partial w_{xy}^1}\\
&=-\eta.{(-(t - r_{fc}).w_{fc}.(\sum_{a=0,b=0}^{a=n,b=n} {w_{ab}.i_{pq}}))}\text { (from eq.(4.4))} \\
&=\eta.{((t - r_{fc}).w_{fc}.(\sum_{a=0,b=0}^{a=n,b=n} {w_{ab}.i_{pq}}))}\\
\Rightarrow w_{xy}^1 &= w_{xy}^1 + \Delta w_{xy}^1
\end{align}
$$
Similar equation to update weights \(w_{00}\) through \(w_{11}\) is provided in part-II.

In next part, we look at a CNN with multiple convolutional and ReLu layers in parallel.

Love or hate this article ? Have other ideas ? Please leave a comment below !