Chaitanya Belwal's Blog

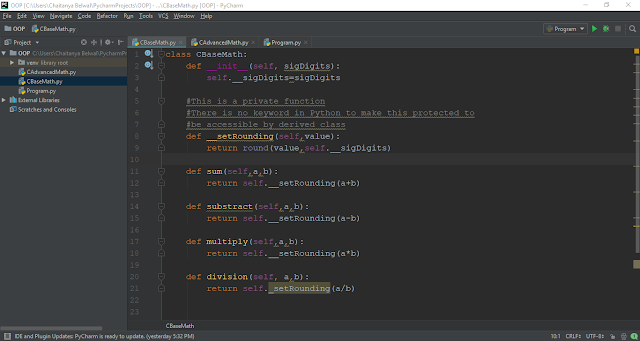
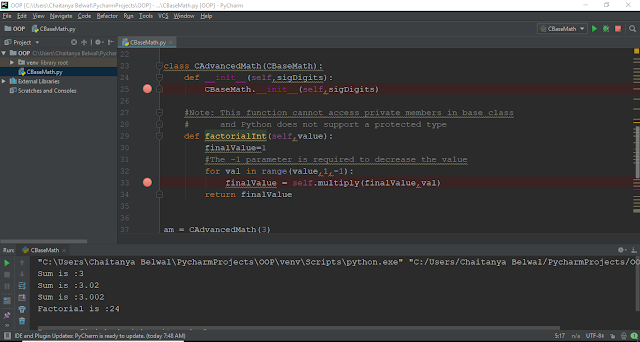
In this article, we take a look at the major control statements in Python. Primary we look at the control statements if-elif-else, for,while and control exit statement break . We list sample code for each of these and use in-line comments to explain what the code line does. Note that we declare the same functions in a class to adhere to object-oriented semantics. You can easily copy/paste the code in your Python code. if-elif-else statement class DemoClass: def IfThenElse(self): # Using integer inp = int(input("Enter a number: ")) if inp The output for the above code is: Sum is :3 Enter a number: 12 Number is positive Enter your name: Chaitanya You are nobody ! for loop class DemoClass: def ForLoop(self): # Print values from 0 to 5 for value in range(6): print(value) # Print values from 1 to 5 for value in range(1,6): print(value) # Print values from 1 to 5, step of 2...

In part-II of this series, we saw how inheritance works when we derive from a single base class. In part-II, the base and derived classes were all declared in the same file. In this article, we look at how classes can be declared in their own files and how they reference each other. The ability to reference source code in multiple files is a very important requirement towards building complex scalable applications. Our project solution will the have following 3 files: Python C# Comments CBaseMath.py CBaseMath.cs Base class code CAdvancedMath.py CAdvancedMath.cs Derived class code Program.py Program.cs Code to instantiate and call functions The code for each of these files is given below: CBaseMath.py / CBaseMath.cs Python class CBaseMath: def __init__(self, sigDigits): self.__sigDigits=sigDigits #This is a private function #There is no keyword in Python to make this protec...

Backpropagation in Neural Networks (NN) is a critical step in adjusting the weights of each layer and making the NN model more accurate based on the provided training data. In previous articles , we derived the backpropagation for a Neural Networks using the architecture of the network. In this series of articles, we convert the neural network architecture into a representative linear equation and use it to derive the backpropagation. As in other articles, we start with a very simple NN and proceed to more complex NN in subsequent articles. Consider the NN below with 1 hidden layer and only a single neuron in each layer. We have derived the backpropagation of this NN without using the equation form here . The output of this NN is \(r_o\), and the prediction error for each training sample \(E\) is defined as: $$ E = {(t - r_o)^2\over 2} \text { ...eq.(1.1)} $$ where t is given(expected) output for that specific training example. Our goal is minimize \(E\) by making \(r_o...

In part-III of this series, we derived the weight update equation for the backpropagation operation of a simple Convolutional Neural Network (CNN) using 3 inputs matrices representing the red, blue and green spectrum of an image. In this article, we derive the backpropagation with 2 consecutive convolution and ReLu layers, and subsequently derive a general backpropagation equation for deep-learning (multi-layered) CNN. To keep our equations simple (and readable), we revert back to only 1 input matrix. This CNN is similar to one used in part-II, except there are 2 convolution and ReLu layers. The CNN we use is represented by: In this CNN, there are 1 4x4 input matrices, two 2x2 filter matrices (or kernels), two convolution layers , two ReLu layers, a single pooling layer (which applies the MaxPool function) and a single fully connected (FC) layer. The elements of the filter matrices are equivalent to the unit weights in a standard NN and will be updated during the backpropaga...

In part-I of this series, we built a basic class in Python and compared the code with a similar class in C#. In this article, we derive the basic class built in part-I to create a new CAdvancedMath to which we add a function to find the factorial of an integer number. The base class code for Python and C# that we used in part-I is given below: Python class CBaseMath: #Constructor class CBaseMath: def __init__(self, sigDigits): self.__sigDigits=sigDigits #This is a private function #There is no keyword in Python to make this protected to #be accessible by derived class def __setRounding(self,value): return round(value,self.__sigDigits) def sum(self,a,b): return self.__setRounding(a+b) def substract(self,a,b): return self.__setRounding(a-b) def multiply(self,a,b): return self.__setRounding(a*b) def division(self, a,b): return self._setRounding(a/b) C# usi...

Due to its simplicity and versatility, Python has become a very popular language among professional software developers and non-developers alike. Python supports the imperative semantics of programming though it has reasonable support for functional programming. In the imperative semantics of programming, Python allows for both procedural (C-style) as well as object-oriented (C++/C#/Java style) programming. While the procedural style of programming in Python is simple and does not use specific semantics, the object-oriented (OO) style does have a small learning curve which in understanding Python specific syntax. Note that just like in C and other procedural languages, the procedural style is a subset of the OO style, implying that all rules/syntax for procedural style apply in OO style. In this article, we look at object-oriented programming in Python. We use a simple example and also compare the similar code in C#. The reason for choosing C# is that the language is a cross betwe...